A Cube Has 12 Of Them: Exploring The Fascinating Properties Of A Cube

Duncan Paucek PhD 05 Jun 2025

When we talk about geometry, a cube is one of the most intriguing three-dimensional shapes. A cube has 12 edges, and each edge plays a crucial role in defining its structure. Understanding the edges of a cube is essential for anyone interested in mathematics, architecture, or design. In this article, we will delve deep into the properties of a cube, focusing on its edges and how they contribute to its unique form.

Geometry is not just about numbers and formulas; it's about understanding the world around us. From the buildings we live in to the objects we use daily, geometry shapes our reality. A cube, with its 12 edges, is a perfect example of symmetry and balance in geometry.

Whether you're a student, a professional, or simply someone curious about the world of shapes, this article will provide you with a comprehensive understanding of the properties of a cube. So, let's dive in and explore the fascinating world of cubes and their edges.

What is a Cube?

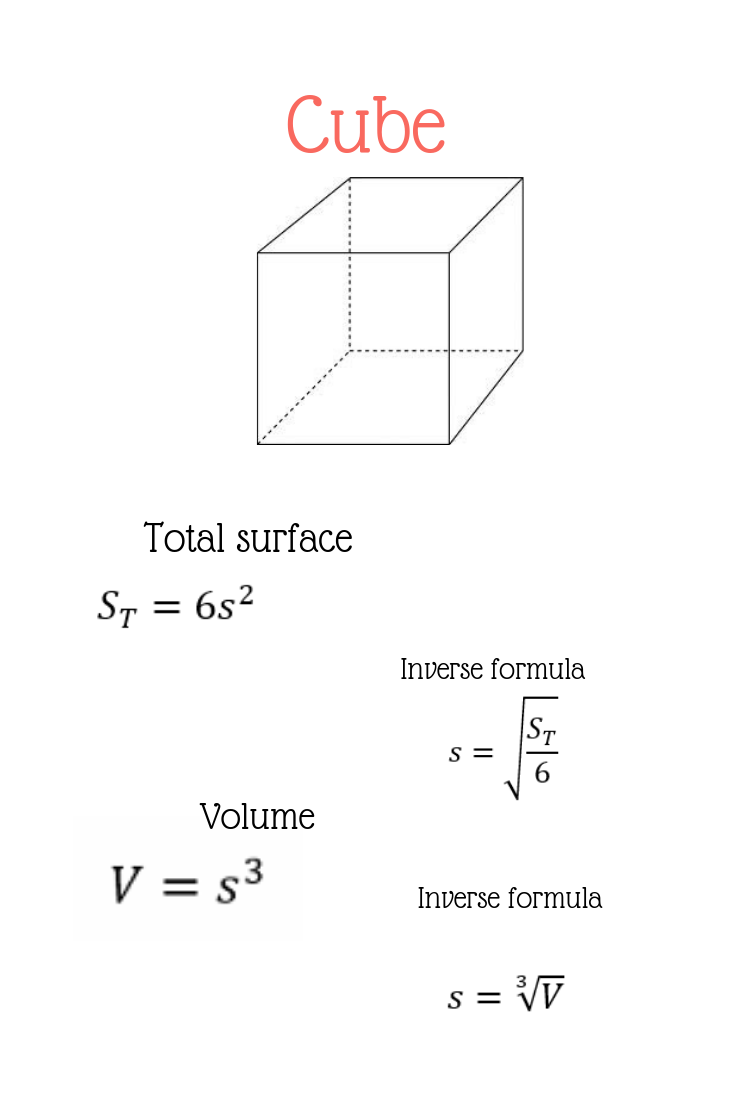
A cube is a three-dimensional solid object bounded by six square faces, with three meeting at each vertex. It is one of the five Platonic solids and is widely studied in geometry. The term "cube" originates from the Greek word "kubos," which means "a die." This shape is ubiquitous in our daily lives, from dice in board games to ice cubes in our drinks.

Understanding the Edges of a Cube

A cube has 12 edges, and these edges are the line segments where two faces meet. Each edge is of equal length, contributing to the symmetry of the cube. Understanding the edges is crucial for comprehending the overall structure of the cube.

How Many Edges Does a Cube Have?

As mentioned earlier, a cube has 12 edges. These edges form the framework of the cube, connecting its vertices and defining its shape. Each edge is shared by two adjacent faces, ensuring the cube's stability and symmetry.

The Importance of Edges in Geometry

In geometry, edges are fundamental components of three-dimensional shapes. They define the boundaries of a shape and play a critical role in determining its properties. For a cube, the 12 edges are essential for maintaining its structure and symmetry.

Applications of Cube Edges in Real Life

Architecture: Architects use the principles of cubes and their edges to design buildings with symmetry and balance.
Engineering: Engineers rely on the properties of cubes to create stable structures in various applications.
Art and Design: Artists and designers use cubes as inspiration for creating aesthetically pleasing works.

Properties of a Cube

Beyond its edges, a cube has several other properties that make it unique. It has six square faces, eight vertices, and all its angles are right angles. These properties make the cube a fascinating subject of study in mathematics and beyond.

Mathematical Representation of a Cube

In mathematical terms, a cube can be represented as a regular hexahedron. Its volume is calculated by cubing the length of one of its edges, and its surface area is calculated by multiplying the area of one face by six.

Exploring the Symmetry of a Cube

Symmetry is one of the defining characteristics of a cube. With 12 edges, six faces, and eight vertices, a cube exhibits perfect symmetry. This symmetry makes it a popular choice in various fields, from art to science.

Types of Symmetry in a Cube

Reflectional Symmetry: A cube can be divided into two identical halves by any plane passing through its center.
Rotational Symmetry: A cube can be rotated around its axes and still maintain its shape and appearance.

Historical Significance of Cubes

Cubes have been studied and admired for centuries. From ancient civilizations to modern times, the cube has held a special place in mathematics and art. The Greeks, for example, considered the cube one of the five Platonic solids, symbolizing the element earth.

Famous Uses of Cubes in History

Pyramids: Ancient Egyptian pyramids were built with cubic stones, showcasing the importance of cubes in construction.
Renaissance Art: Artists during the Renaissance used cubes to study perspective and create realistic paintings.

Modern Applications of Cubes

In today's world, cubes continue to play a vital role in various fields. From computer graphics to quantum mechanics, the properties of cubes are utilized in innovative ways.

Examples of Modern Cube Applications

Computer Graphics: Cubes are used as basic building blocks in 3D modeling and animation.
Quantum Computing: Researchers use cube-like structures to model quantum states and interactions.

Fun Facts About Cubes

Cubes are not just mathematical objects; they are also fascinating in their own right. Here are some fun facts about cubes:

A cube is the only Platonic solid that can tessellate space without gaps.
The Rubik's Cube, a popular puzzle toy, is based on the structure of a cube.

Conclusion

In conclusion, a cube has 12 edges, and these edges are essential for defining its structure and symmetry. From its historical significance to its modern applications, the cube remains a captivating subject of study. Whether you're exploring geometry, architecture, or art, understanding the properties of a cube can enrich your knowledge and appreciation of the world around us.

We invite you to share your thoughts and questions in the comments below. Feel free to explore other articles on our site for more fascinating insights into the world of mathematics and geometry. Together, let's continue to learn and grow!

What is a Cube?
Understanding the Edges of a Cube
The Importance of Edges in Geometry
Properties of a Cube
Exploring the Symmetry of a Cube
Historical Significance of Cubes
Modern Applications of Cubes
Fun Facts About Cubes
Conclusion

References:

Euclid's Elements
Plato's Timaeus
Modern Geometry Textbooks

Cube matemaths

Solved A cube has 4cm by 4cm faces. What is the cube’s surface area

Fame Game