P Power Sample: A Comprehensive Guide To Understanding And Utilizing Statistical Power
Statistical power, often referred to as P power sample, plays a crucial role in research and data analysis. It is a fundamental concept that helps researchers determine the likelihood of detecting an effect when there is one. Without adequate power, studies may fail to produce reliable results, leading to wasted resources and misleading conclusions.
In today's data-driven world, understanding statistical power is more important than ever. Researchers, statisticians, and analysts rely on P power sample to design studies that yield meaningful insights. This guide aims to provide an in-depth exploration of the concept, ensuring that you have all the tools and knowledge necessary to apply it effectively in your work.
Whether you're a student learning about statistical methods or a professional conducting advanced research, this article will cover everything you need to know about P power sample. From basic definitions to practical applications, we'll walk you through the essential elements of this critical concept.
What is P Power Sample?
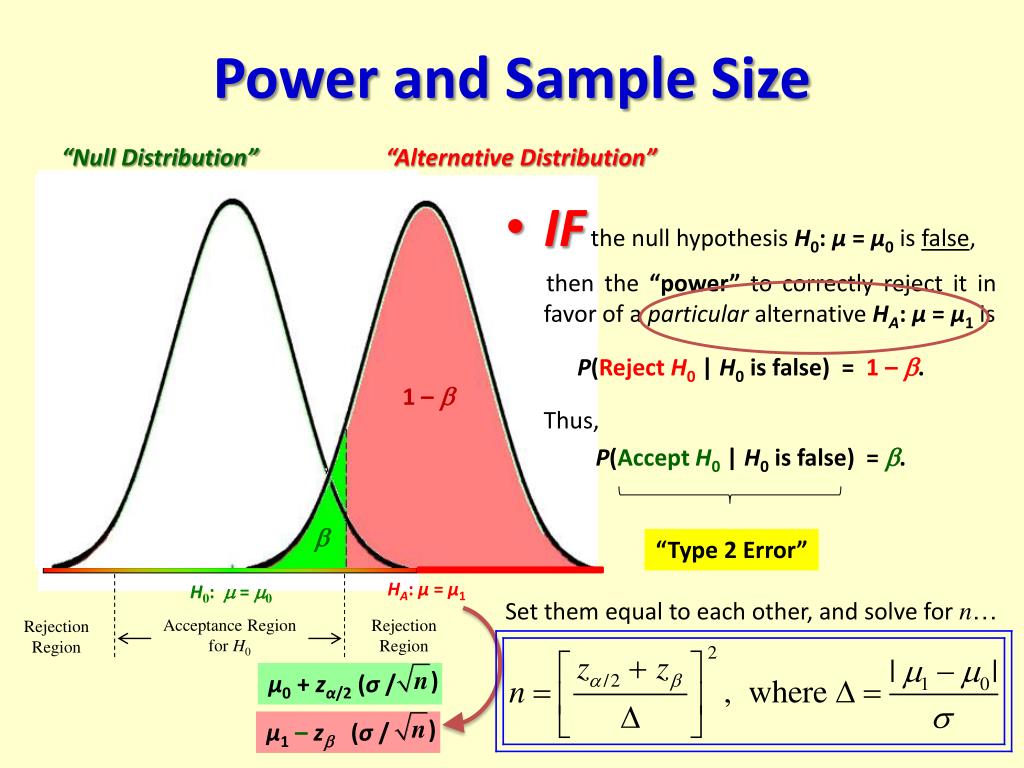
P power sample refers to the probability of correctly rejecting a null hypothesis when the alternative hypothesis is true. In simpler terms, it measures the likelihood of detecting an effect if one truly exists. Statistical power is a key component of hypothesis testing, ensuring that studies are designed with sufficient sensitivity to identify significant results.
Statistical power is influenced by several factors, including:
- Effect size: The magnitude of the effect being studied.
- Sample size: The number of observations or participants in the study.
- Significance level (alpha): The threshold for rejecting the null hypothesis.
- Variability: The degree of spread or dispersion in the data.
By optimizing these factors, researchers can increase the power of their studies and improve the reliability of their findings.
Why is P Power Sample Important?
Understanding P power sample is critical for ensuring the validity and reliability of research studies. Studies with low power are more likely to produce false negatives, where real effects are missed. This can lead to wasted resources, incorrect conclusions, and a lack of confidence in the results.
Impact on Research Design
P power sample directly impacts the design of research studies. Researchers must carefully consider the required sample size and effect size to achieve adequate power. This ensures that the study is both efficient and effective in detecting meaningful effects.
Implications for Decision-Making
In fields such as medicine, psychology, and economics, the consequences of low statistical power can be significant. Decisions based on underpowered studies may lead to ineffective treatments, misguided policies, or missed opportunities for innovation. By prioritizing P power sample, researchers can enhance the quality of their work and contribute to better decision-making.
Factors Affecting P Power Sample
Several factors influence the power of a statistical test. Understanding these factors is essential for designing studies with sufficient power. Below are the key elements to consider:
- Effect size: Larger effect sizes increase the power of a test, making it easier to detect significant results.
- Sample size: Larger samples generally lead to greater power, as they reduce the impact of random variation.
- Significance level: Lower significance levels (e.g., 0.01 instead of 0.05) decrease power, as they require stronger evidence to reject the null hypothesis.
- Variability: Reducing variability in the data can increase power by making it easier to detect effects.
By carefully managing these factors, researchers can optimize the power of their studies and improve the likelihood of detecting true effects.
How to Calculate P Power Sample
Calculating P power sample involves several steps and requires an understanding of statistical concepts. Below is a step-by-step guide to help you calculate power:
Step 1: Define the Null and Alternative Hypotheses
Start by clearly defining the null and alternative hypotheses. The null hypothesis typically assumes no effect or difference, while the alternative hypothesis states the expected effect or difference.
Step 2: Determine the Significance Level
Choose a significance level (alpha) for your test. Common values include 0.05, 0.01, and 0.10. The significance level represents the threshold for rejecting the null hypothesis.
Step 3: Estimate the Effect Size
Estimate the expected effect size based on prior research or theoretical considerations. Effect sizes can be expressed in various ways, such as Cohen's d, correlation coefficients, or odds ratios.
Step 4: Calculate Power
Use statistical software or power tables to calculate the power of your test. Input the sample size, effect size, significance level, and other relevant parameters to obtain the power value.
Common Misconceptions About P Power Sample
Despite its importance, P power sample is often misunderstood by researchers and practitioners. Below are some common misconceptions and clarifications:
- Higher power always means better results: While higher power increases the likelihood of detecting effects, it does not guarantee better results. Other factors, such as study design and data quality, also play a critical role.
- Power is only relevant for large studies: Even small studies can benefit from power analysis, as it helps ensure that the sample size is sufficient to detect meaningful effects.
- Power is fixed once a study begins: Power can be adjusted during the study design phase, but it becomes fixed once data collection begins. Proper planning is essential to avoid underpowered studies.
By addressing these misconceptions, researchers can better understand the role of P power sample in their work and make more informed decisions.
Practical Applications of P Power Sample
P power sample has numerous practical applications across various fields. Below are some examples:
1. Clinical Trials
In clinical trials, P power sample ensures that studies are designed to detect treatment effects with sufficient confidence. This is crucial for determining the efficacy and safety of new drugs or therapies.
2. Social Sciences
In the social sciences, P power sample helps researchers identify meaningful relationships between variables. This is particularly important in fields such as psychology, sociology, and education, where complex phenomena are studied.
3. Business and Economics
In business and economics, P power sample is used to evaluate the impact of interventions, policies, or market changes. This helps organizations make data-driven decisions and optimize their strategies.
Best Practices for Maximizing P Power Sample
To maximize the power of your studies, consider the following best practices:
- Conduct a power analysis during the study design phase to determine the required sample size.
- Minimize variability in the data by using consistent measurement methods and controlling for confounding variables.
- Choose an appropriate significance level based on the context and goals of your study.
- Use statistical software or power tables to calculate power accurately and efficiently.
By following these best practices, researchers can enhance the power of their studies and improve the reliability of their results.
Challenges in Achieving Adequate P Power Sample
Achieving adequate P power sample can be challenging due to various constraints and limitations. Below are some common challenges and potential solutions:
1. Limited Resources
Resource constraints, such as budget or time limitations, can make it difficult to achieve sufficient sample sizes. Researchers can address this by prioritizing key variables, using efficient sampling methods, or leveraging existing datasets.
2. Small Effect Sizes
Studies with small effect sizes require larger sample sizes to achieve adequate power. Researchers can overcome this by using more sensitive measurement instruments or combining multiple studies through meta-analysis.
3. High Variability
High variability in the data can reduce the power of a study. Researchers can minimize variability by controlling for confounding factors, using stratified sampling, or employing advanced statistical techniques.
Conclusion
P power sample is a critical concept in research and data analysis, ensuring that studies are designed with sufficient sensitivity to detect meaningful effects. By understanding the factors that influence power and following best practices, researchers can enhance the quality and reliability of their work.
We invite you to share your thoughts and experiences with P power sample in the comments section below. Additionally, feel free to explore other articles on our site for more insights into statistical methods and research design. Together, we can advance the field of data analysis and contribute to better decision-making in various domains.
Table of Contents
- What is P Power Sample?
- Why is P Power Sample Important?
- Factors Affecting P Power Sample
- How to Calculate P Power Sample
- Common Misconceptions About P Power Sample
- Practical Applications of P Power Sample
- Best Practices for Maximizing P Power Sample
- Challenges in Achieving Adequate P Power Sample
- Conclusion

PPT Introduction to sample size and power calculations PowerPoint
PPT Power and Sample Size PowerPoint Presentation, free download ID